什么是倍频程分析？它解决了什么问题？

倍频程（Octave）分析是一类“按对数频率划分”的谱分析方法：把频率轴分成若干个带通频带（band），每个频带的上截止频率与下截止频率之比恒定（常数比例带宽，Constant Percentage Bandwidth, CPB）。在每个频带内，我们不关心更细的线谱结构，而关注该频带内的总能量/均方根（RMS）或功率。

• 它不是“看每个 Hz 发生了什么”，而是“看每一段相对带宽内的能量如何分布”
• 它天然适配人耳与很多工程系统：对频率的分辨能力常更接近“相对尺度”（例如 1 kHz 与 1.1 kHz 的差异），而非固定 1 Hz 的差异
• 它是许多标准规定的报告格式：房间声学参数、隔声评价、环境噪声、机器噪声、风噪/路噪等常用 1/3 倍频程

从“线性 Hz”到“对数频率”：为何 CPB 更像工程语言

用等宽频带（例如每 10 Hz 一个桶）统计能量，会导致：
• 在低频：10 Hz 的桶可能过宽，掩盖细节
• 在高频：10 Hz 的桶又过窄，统计方差大、对随机噪声不稳定
而 CPB 的带宽随频率增长（Δf ∝ f），使得每个频带覆盖“相近的相对变化”，因此更稳定，也更符合很多标准化测试的可重复性要求。

直观看带宽如何随频率增长

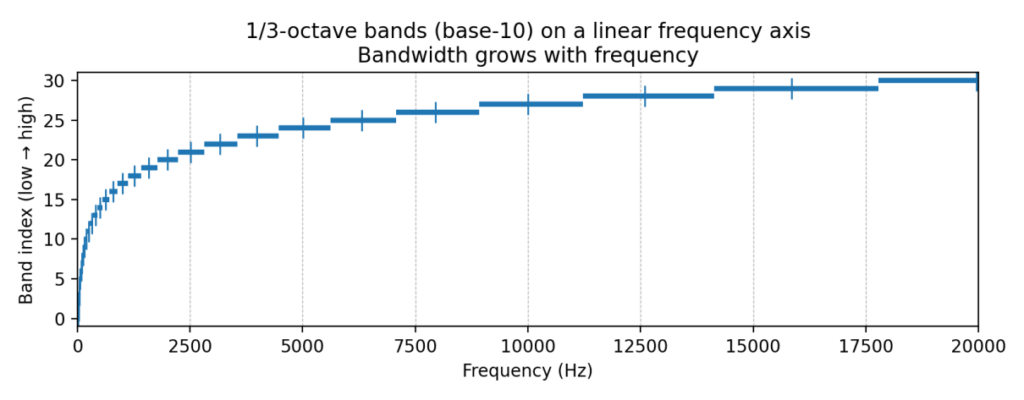
图 1：同样的 1/3 倍频程频带，在“线性频率轴”上看，带宽会随频率增大

每条横线代表一个 1/3 倍频程频带 [f1, f2]；短竖线表示中心频率 fm。在线性坐标下，频带在高频处看起来更“宽”。

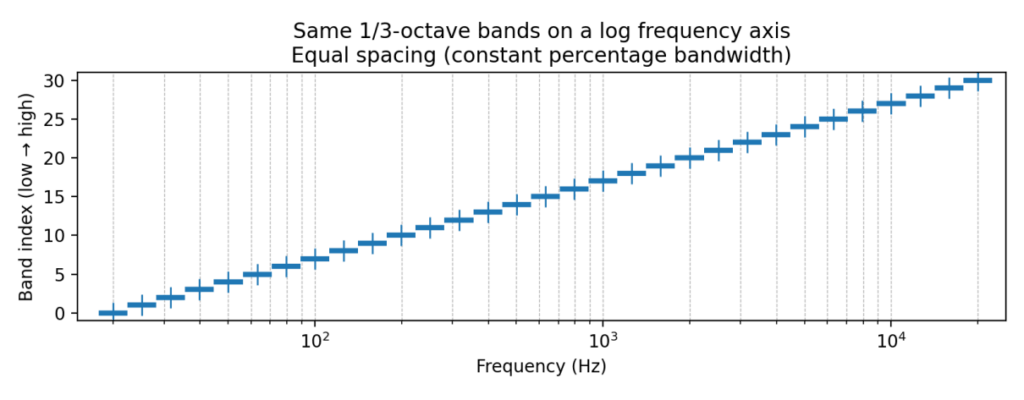
图 2：同样的频带放到“对数频率轴”上看，会出现等间距的频带结构（常数百分比带宽）

把横轴改为对数刻度后，这些同样的频带在视觉上呈“等宽/等间距”，这正是常数百分比带宽（CPB）的本质。

这两张图解释了倍频程的核心：它不是“频带更宽/更窄”，而是“以对数尺度为等距单位”。

标准与术语：IEC/ANSI/ISO 体系到底规定了什么？

工程上说“做 1/3 倍频程”，真正的约束不只是频带边界，还包括：中心频率的定义（exact vs nominal）、倍频程比（base-10 vs base-2）、滤波器幅频容差（class）、以及输出量的口径（带内能量如何定义、时间平均怎么做、校准如何处理）。

IEC 61260-1:2014 的关键点：base-10 倍频程比、参考频率与中心频率公式

IEC 61260-1:2014 是倍频程/分数倍频程滤波器的核心规格标准之一。它明确采用 base-10 设计：倍频程比 G 定义为 G = 10^(3/10) ≈ 1.99526（非常接近 2，但不是严格 2）。参考频率 fr = 1000 Hz。标准给出 exact mid-band frequency（精确中心频率）的生成公式，并强调 band-edge frequencies 的几何均值等于中心频率。 [1]

IEC 61260-1 (base-10) 关键公式（摘录并整理，见 [1]）：

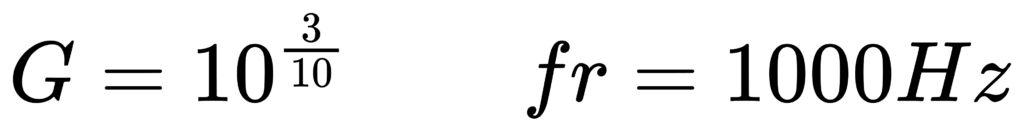
当 1/b 的分母 b 为奇数（例如 1,3,5,…）时：

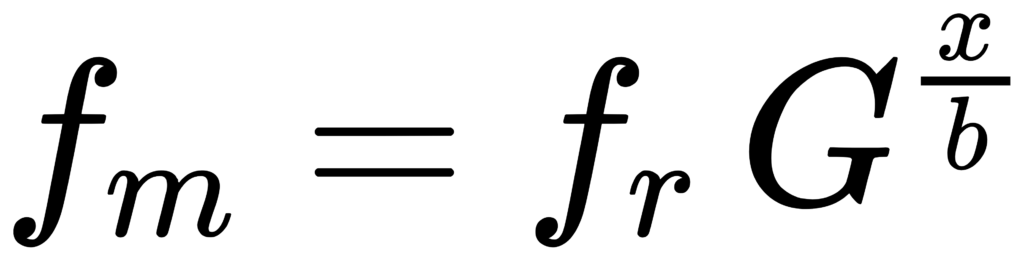
当 b 为偶数（例如 2,4,6,…）时：

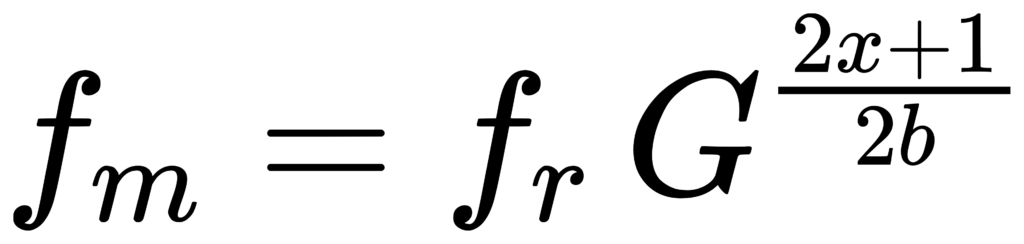
此外：

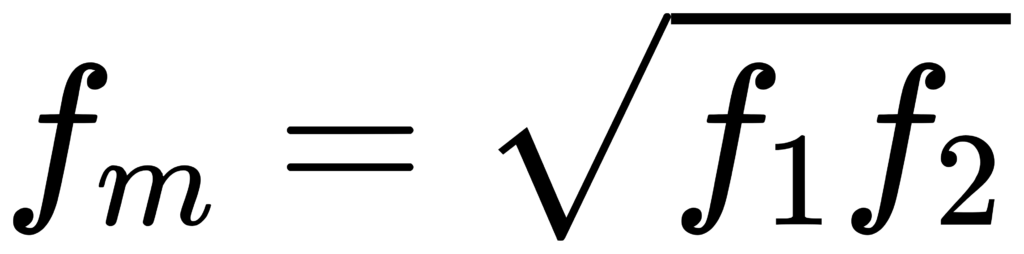
使用OpenTest的IEC 61260-1倍频程分析功能观察数据->

为什么偶数 b 的公式会“半步错开”？

你可以把中心频率序列想成在 log(f) 轴上的“等间距刻度”。当 b 为奇数时（如 1、3），标准把参考频率 fr=1000 Hz 直接放在某个刻度点上，所以 1000 Hz 本身就是一个中心频率（x=0）。
当 b 为偶数时（如 2、4），如果仍然让 1000 Hz 落在刻度点上，会导致频带边界（f1、f2）在一些场景下不够“对称/整齐”（特别是你希望某些报告频率刚好落在边界上）。因此标准选择把中心频率序列整体在 log 轴上平移半个间隔：中心频率落在“半格”位置，而 1000 Hz 会更接近成为两个相邻中心频率之间的几何中点（也就是某些频带边界更容易对齐）。
从公式上看，这个“半格平移”就是 (2x+1)/(2b) 这种写法：它保证相邻中心频率的比值仍然是 G^(1/b)，只是把整个序列相对参考频率做了 1/(2b) 的指数偏移。

工程上你不必死记偶数/奇数两套式子——更稳妥的做法是：
1) 先用标准给出的中心频率公式生成 exact fm 序列；
2) 再用 f1 = fm / G^(1/(2b))、f2 = fm * G^(1/(2b)) 得到边界；
3) 最后把 fm 显示为常用 nominal（例如 1 kHz、1.25 kHz、1.6 kHz）。
这样实现出来的频带一定在数学上自洽，也最不容易和标准“走偏”。

工程解释：
• 公式决定了“中心频率序列”的对数等比性质；
• 几何均值定义保证频带在对数轴上关于中心对称；
• 选择 base-10 意味着序列与十进制优选数（ISO 3/ISO 266）更自然对齐。 [1][2]

频带边界、中心频率、带宽设计器 b：从定义到可计算

标准术语中常见 1/b 作为“带宽设计器（bandwidth designator）”：例如 1/1 为 1 倍频程，1/3 为 1/3 倍频程。 [1]
一旦你选定 (G, b, fr)，整套频带就被数学上锁定：每个频带的中心频率 fm 与边界 (f1,f2) 都是可计算的。

exact vs nominal：为什么同一个频带会出现两个“中心频率”？

在标准里，“精确中心频率（exact）”用于数学一致性与滤波器设计；“标称中心频率（nominal）”用于标注、报告与工程交流。 [1]
ISO 266:1997 给出了声学测量的优选频率（preferred frequencies），以 1000 Hz 为参考，并基于 ISO 3 的 R10 优选数列。 [2]
因此，1/3 倍频程的 exact 序列（严格等比）会被舍入成一串非常常见的标称值：
20, 25, 31.5, 40, 50, 63, 80, 100, 125, 160, … , 1k, 1.25k, 1.6k, 2k, 2.5k, 3.15k, … , 20k。

• 工程上“31.5 Hz”“6.3 kHz”“12.5 kHz”等标称值来自 R10 系列的习惯写法，利于读写与表格化。
• 算法实现应优先用 exact 频率计算边界，再将结果标注为 nominal；这样最不容易出错。

base-10 vs base-2：为何标准不坚持严格 2:1？

许多人对 octave 的直觉是 2:1。IEC 61260-1 采用 base-10（G=10^(3/10)）而不是 base-2（G=2）的主要原因：
• 与十进制优选数列对齐（ISO 266 直接基于 R10 系列）。 [2]
• 统一国际标准：IEC 61260-1:2014 只规定 base-10，并提示 base-2 设计在远离参考频率时符合标准的概率会降低。 [1]
数学上：log10(2) ≈ 0.3010，1/3 octave 在对数十进制上接近 0.1 decade；而 base-10 定义直接令相邻 1/3 带比值为 10^(1/10)，使得每个 decade 恰好 10 个 1/3 带，这是与 R10 的“漂亮对齐”。

“10 个 1/3 带 = 1 个 decade”：这件事为什么很重要？

当 1/3 倍频程按 base-10 定义时，相邻中心频率比值 r = 10^(1/10)。因此：
• 每走 10 个 1/3 带，频率正好乘以 10（一个 decade）；
• 这与 ISO 266 的 R10 优选数列天然一致；
• 这让很多工程表格、标称频率、图纸标注非常顺手。
从标准化角度看，“易读、易写、易比对”是极其重要的工程价值：它减少沟通成本与误用概率。

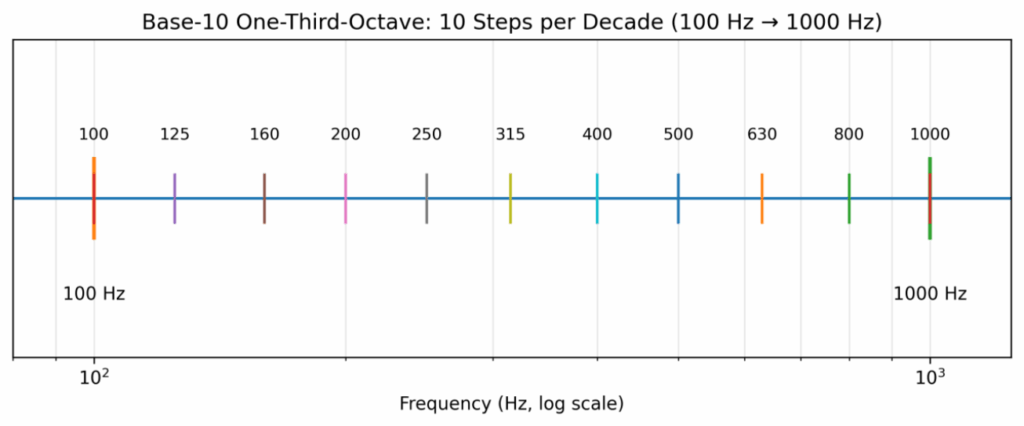
图 3：Base-10 1/3 倍频程在一个 decade（10× 频率）内的 10 个等比步进示意

ANSI S1.11 / ANSI/ASA S1.11：容差等级（class）与瞬态提醒

ANSI S1.11 及其采用 IEC 61260-1 的版本同样描述了滤波器组/频谱分析仪所需的性能要求，并引入不同容差等级（例如一些版本包含 class 0/1/2）。 [3][4]
一个非常工程化的提醒是：标准指出对于瞬态信号，不同实现的滤波器（即便都满足同一规范）可能给出不同结果。 [3]这意味着：当你把倍频程用于瞬态诊断时，必须关注“算法的时间响应”。

“class / mask / effective bandwidth”到底在管什么？

很多人以为“做了 1/3 倍频程”只要频带边界对了就行，但在标准化测量里更关键的是：不同设备/算法要得到可比结果。这就需要把滤波器/分析器的行为约束到一个“允许的范围”里——这就是 IEC/ANSI 里常说的 class（等级）和 mask（容差掩模）的意义。

可以把它拆成三层去理解：
• 频率划分（frequency spacing）：中心频率序列与边界如何定义（base-10、exact/nominal、f1/f2）。
• 幅频响应容差（magnitude response mask）：在通带附近允许多大起伏？离中心频率多远必须衰减到多小？（用于保证邻带隔离与一致性）
• 能量口径一致性（effective bandwidth）：面对宽带随机噪声时，‘通过滤波器后得到的均方值’必须在设备间可比。

为什么要强调 effective bandwidth？因为真实滤波器不是“理想砖墙”。对随机噪声而言，带内输出能量取决于 ∫|H(f)|^2 S(f)df，只要 |H(f)| 的尾巴、滚降、通带起伏不同，即便频带边界名义上相同，带级也会系统性偏差。标准通过对有效带宽/归一化有效带宽的约束，把这种偏差压到可接受的范围内。 [1][3][4]

另外，标准强调“瞬态信号可能导致不同合规实现输出不同”并不是矛盾，而是提醒你：
• mask 主要约束的是稳态频域特性（幅频与带宽），而瞬态还与相位/群延迟、滤波器振铃、以及你选择的时间平均方式有关；
• 所以当你做冲击、扫频、短事件诊断时，必须固定算法细节（滤波器结构、阶数、时间常数、平均窗口）并做基准比对。 [3]

数学基础：1/n 倍频程频带的定义、带宽、Q 值与带编号

CPB（常数百分比带宽）与“对数等距”

CPB 的等价说法是：在对数频率轴上，每个频带的宽度相同。设归一化变量 u = log(f)，那么频带边界对应 u 上的固定间隔。这在噪声与振动工程里很自然：许多谱型（例如 1/f 类谱）在对数尺度上更平滑，统计更稳定。

由几何均值推导边界公式（通用 1/b 形式）

标准给出中心频率是边界的几何均值 fm = sqrt(f1*f2)。 [1]
对 1/b 倍频程，通常取边界比值 f2/f1 = G^(1/b)（G 为倍频程比）。于是：

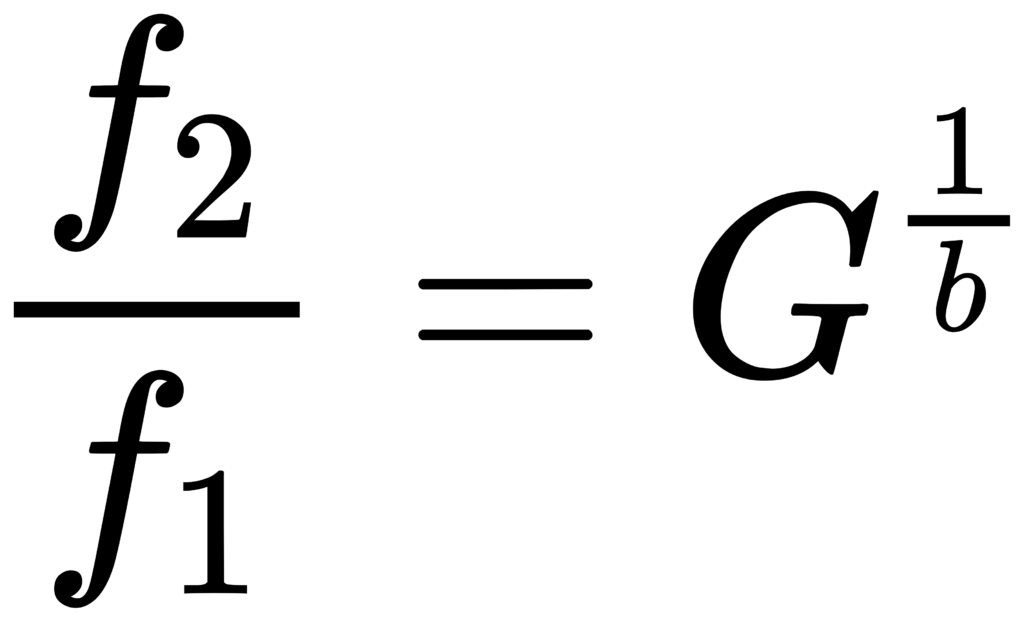
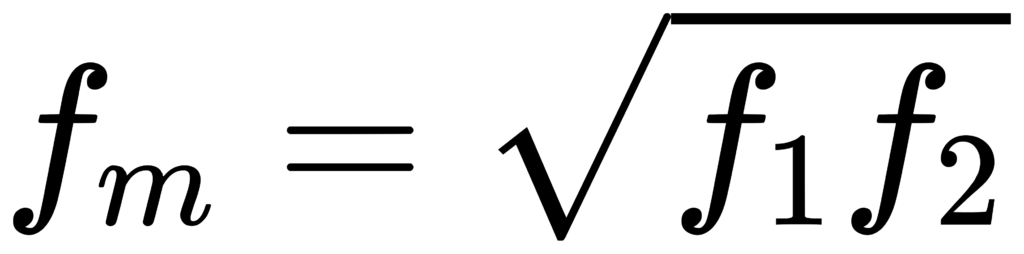
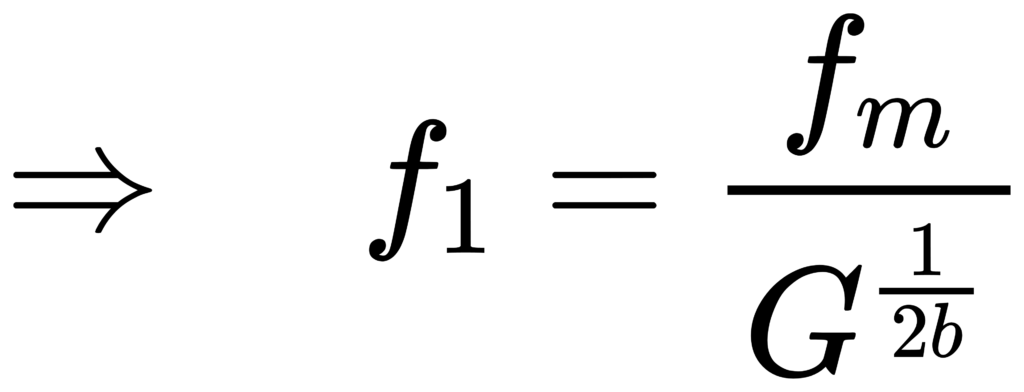
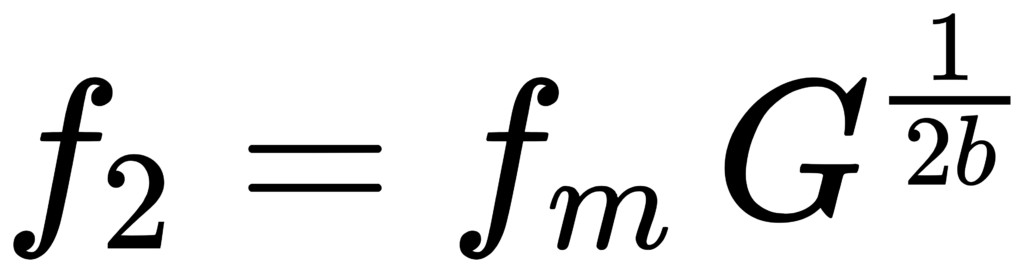
对 base-10 1/3 倍频程：G=10^(3/10), b=3。
相邻中心频率比值 r = G^(1/3) = 10^(1/10) ≈ 1.258925；边界倍数 k = 10^(1/20) ≈ 1.122018。

Q 值与分辨率：倍频程就是常数-Q 分析

Q = fm / (f2 – f1)。对 CPB：Δf = f2-f1 与 fm 成比例，因此 Q 仅由 b 与 G 决定。

设

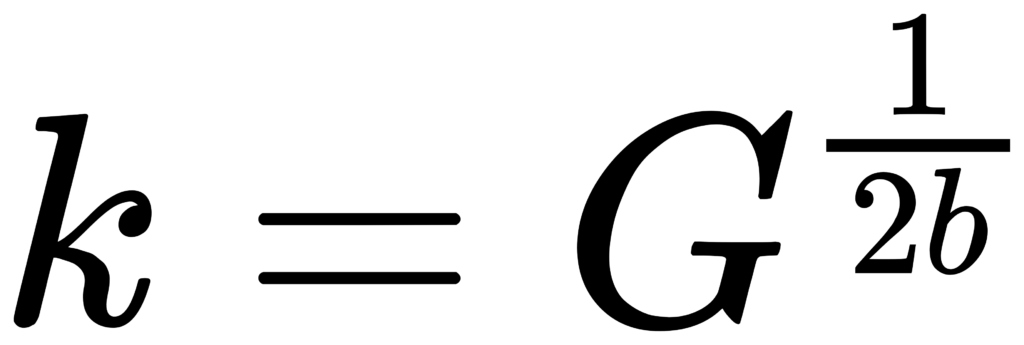
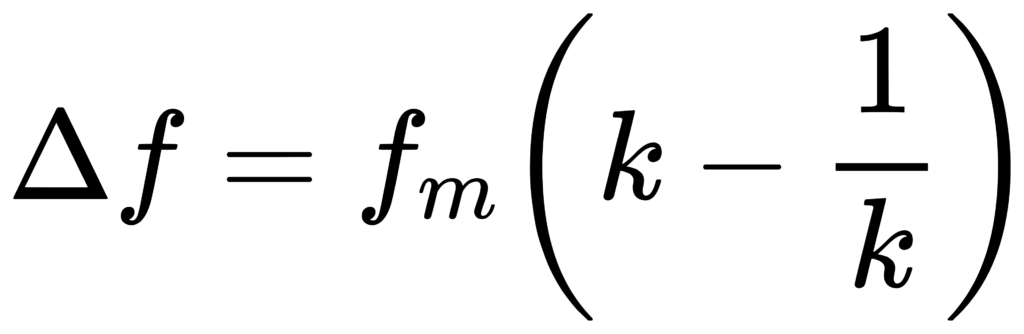
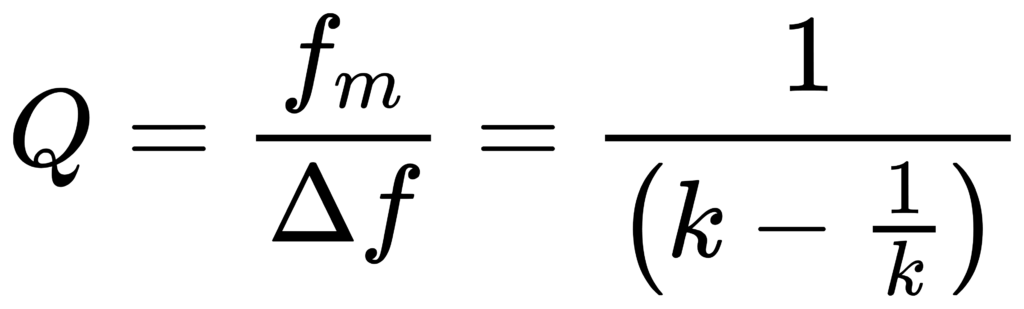
=> Q 与 fm 无关（常数-Q）

工程含义：
• 在低频，频带窄 -> 频率分辨更细；
• 在高频，频带宽 -> 能量统计更稳、对随机噪声更友好。

常见分数倍频程的相对带宽与 Q 值速查（base-10，fr=1000 Hz）：

分数倍频程	频带比值 f2/f1	相对带宽 Δf/fm	Q = fm/Δf
1/1	1.995262	0.704592	1.419
1/2	1.412538	0.347107	2.881
1/3	1.258925	0.230768	4.333
1/6	1.122018	0.115193	8.681
1/12	1.059254	0.057573	17.369

解读：1/3 倍频程的 Q≈4.33，意味着每个频带的带宽大约是中心频率的 23%。分得更细（1/6、1/12）虽然分辨率更高，但对随机噪声的统计方差也会更大、所需平均时间更长。

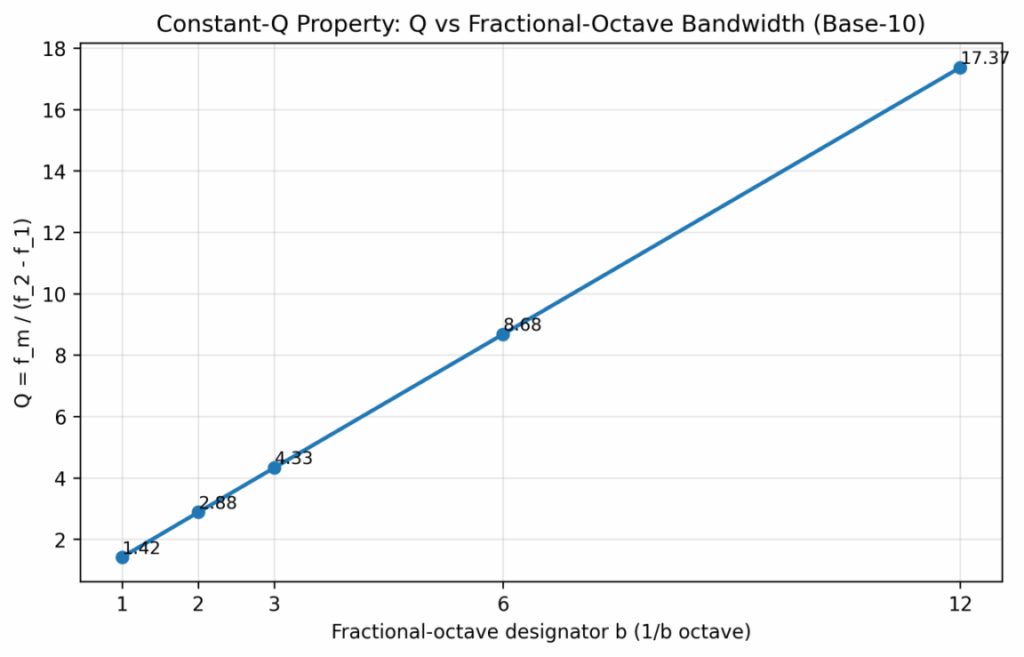
图 4：常见分数倍频程的 Q 值（base-10 定义）

带编号（band number）与公式化索引

实现时经常需要一个整数索引（band number）来枚举频带。IEC 用整数 x 出现在中心频率公式里：fm = fr * G^(x/b)。 [1]
因此你可以反求 x：

给定 fm（exact）：

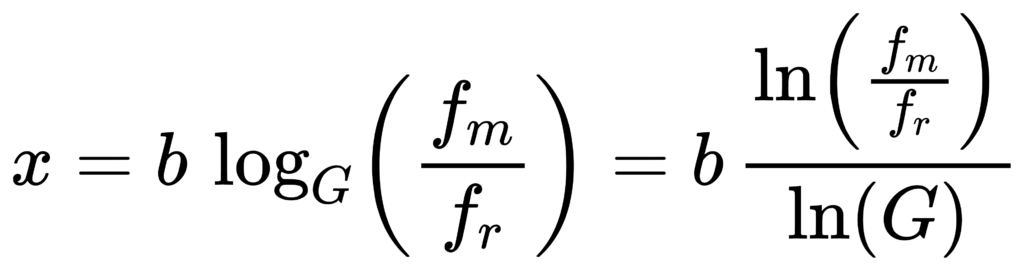
对 base-10：

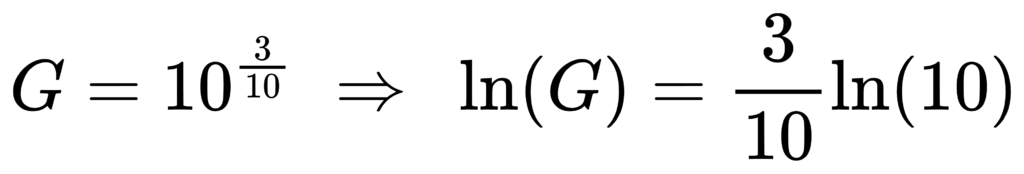
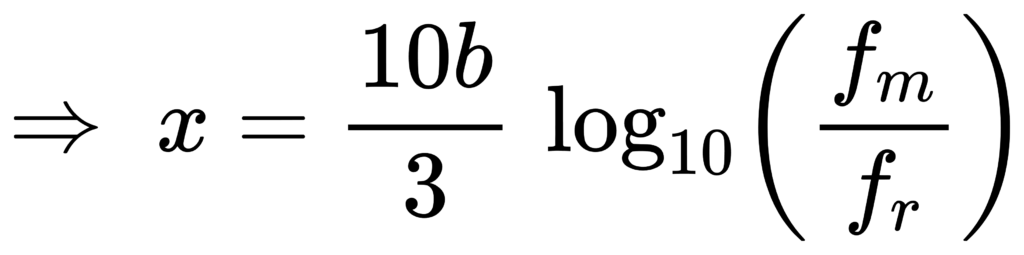
这个索引在工程上很有用：
• 你可以稳定地生成“覆盖某个频率范围”的整套频带；
• 你可以确保频带边界连续（contiguous），且每一带严格对应标准定义。

“1/3 倍频程”的两种口径：base-2 与 base-10（别混用）

在一些文献中，“1/3 octave”可能指 base-2 的 2^(1/3)；而在 IEC 61260-1:2014 的滤波器规范与很多现代声学测量语境中，更常用 base-10 的 10^(1/10)（也可理解为 1/10 decade）。
实际项目里必须确认：你的仪器/软件采用的是哪一种定义。一个简单检查法：看相邻标称中心是否是 1.0k -> 1.25k -> 1.6k -> 2.0k 这种 R10 风格，若是，则大概率是 base-10。

倍频程带级的数学定义：从 PSD 积分到 dB 报告口径

连续频域：带内能量积分

倍频程带级本质是“功率谱密度在频带内积分”。以声压 p(t) 为例：

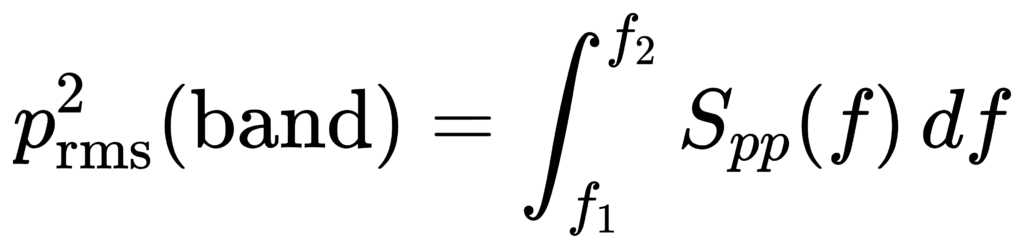
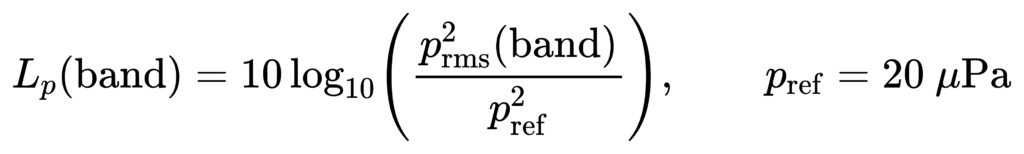
对振动（速度/加速度）完全类似，只是参考量与单位不同。
关键点：dB 是对数，任何求和/平均必须先回到线性功率或均方域。

离散实现的两条路：滤波器输出 RMS vs FFT/PSD 装桶

• 滤波器法：y_b(t)=BandPass_b{x(t)}，然后 p_rms^2(b)=mean(y_b^2)。
• FFT/PSD 法：先估计 S_pp(f)，再对 f∈[f1,f2] 做数值积分（bin 求和）。
• 两者对“长时间平稳信号”的平均结果可非常接近，但对瞬态、扫频、短事件往往不同。

先把“谱是什么”说清楚：幅度谱、功率谱、PSD（以及 dB/Hz）

离散信号做 FFT 后，最容易混淆的是“你手里那条谱到底是什么量”。用声压 p(t) 举例（单位 Pa）：
• 幅度谱 |X(f)|：仍然与‘幅度’同量纲（Pa），常用来观察纯音/谐波。
• 功率谱 |X(f)|^2：量纲变成 Pa^2，直接对应均方（能量）。
• 功率谱密度 PSD：量纲是 Pa^2/Hz，表示‘每 1 Hz 的均方’（噪声分析里最常用）。
倍频程带级本质上是带内均方（Pa^2）或功率的积分/求和，所以无论你从哪条谱出发，最终都必须落回到 Pa^2 的能量域。

频率分辨率与单边谱：Δf、0..fs/2、以及“乘 2”

FFT 的 bin 间隔是 Δf = fs/N。把 PSD 离散化后，带内积分通常近似为：
均方(带) ≈ Σ_{k∈band} PSD[k] · Δf
如果你使用的是‘单边谱’（只保留 0..fs/2），为了能量守恒，除 DC（0 Hz）与 Nyquist（fs/2，若存在）外，通常需要把其余频点的功率乘以 2（因为负频率那一半被折叠掉了）。
很多实现对这一点处理不同，导致同一段数据在不同软件里差一个常数偏移；所以做对比时一定要先把“谱的定义”对齐。

窗函数校正：coherent gain（纯音）与 ENBW（噪声）是两件不同的事

加窗的目的，是降低频谱泄漏（尤其是非整数周期的纯音）。但窗会改变两类量：
• 对纯音幅度：窗会把峰值‘压低’，需要用 coherent gain（CG）校正。常见定义：CG = sum(w)/N。
• 对宽带噪声：窗会改变噪声底的统计平均，需要用等效噪声带宽 ENBW 校正。常见定义：ENBW = fs · sum(w^2)/(sum(w))^2。 [9]
直觉上：CG 关心的是‘峰值高度’，ENBW 关心的是‘噪声底面积’。倍频程带级属于能量统计，更常受 ENBW 影响。

常见窗口速查（典型值，N 足够大时 ENBW 以“bin 宽度”为单位）：

窗口	Coherent Gain CG	ENBW（bins）
Rectangular	1.000	1.000
Hann	0.500	1.500
Hamming	0.540	1.363
Blackman	0.420	1.727

提示：如果你的目标是“噪声带级”，优先确认 ENBW/PSD 口径；如果你的目标是“纯音幅值落在哪个频带”，再去确认 CG 与频谱泄漏。

装桶时的“部分 bin”加权：边界不对齐时怎么做才不跳变

把 PSD 当成在每个 bin 宽度 Δf 内近似常数，那么任意频带 [f1,f2] 的积分可以写成：

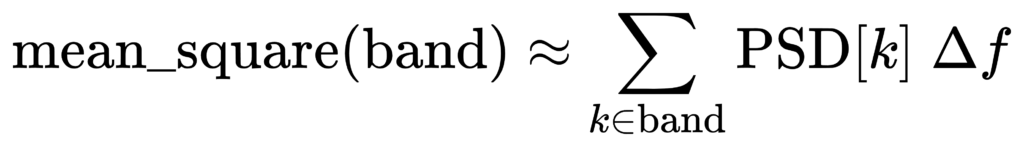
其中 α_k∈[0,1] 是‘该 bin 与频带的重叠比例’：

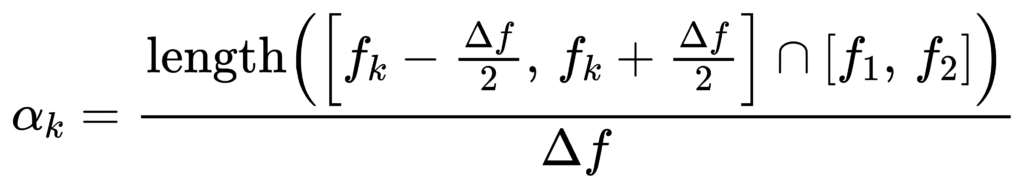
这样做的好处是：当你稍微移动边界或改变 N 时，带级变化会更平滑、更符合连续积分的直觉。

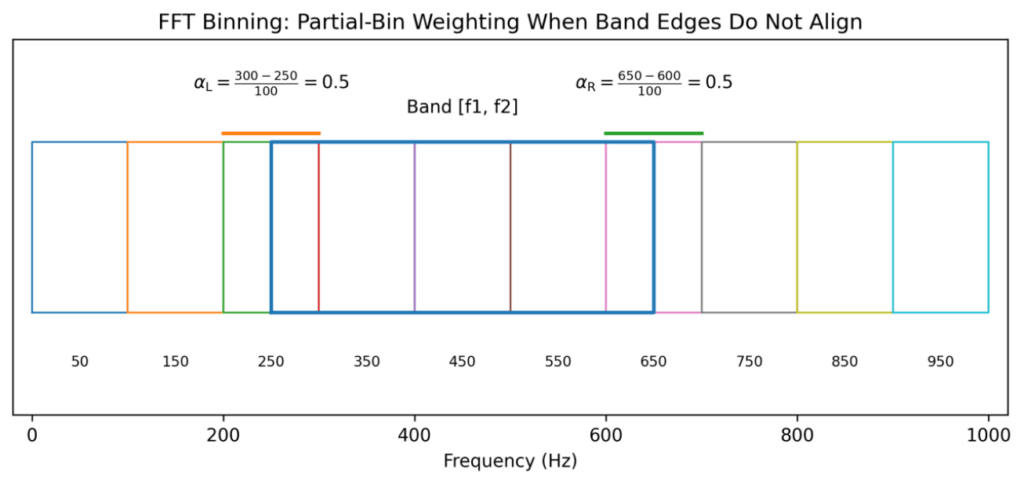
图 5：FFT 装桶时的“部分 bin 加权”示意（频带边界与 FFT bin 不对齐）

两条路什么时候“理论等价”？用一个公式把它们统一起来

严格地说，滤波器法与 PSD 装桶法都在做同一件事：把信号的功率按频率分配并积分。统一写法是：

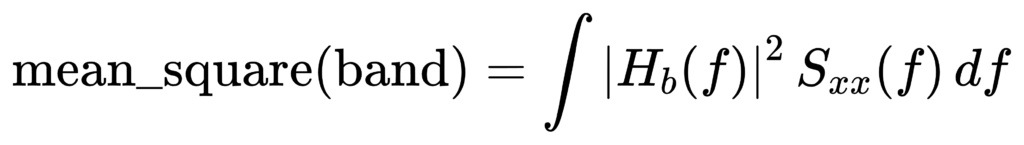
• 若 H_b(f) 是理想砖墙（bandpass=1，bandstop=0），就退化成 ∫_{f1}^{f2} S_xx(f) df。
• 若 H_b(f) 是真实标准滤波器，则积分里会自然包含滚降与通带起伏；这也是为什么标准要约束 |H_b(f)| 与有效带宽。

因此，两条实现想要数值上尽量一致，要么让 FFT 装桶近似同样的 |H_b(f)|（例如用 FFT synthesis 的权重），要么接受它们对‘边界/滚降’的不同处理并在报告中注明方法。

频带合成：从 1/3 倍频程合成 1 倍频程（以及总级）

在理想的频带划分与能量守恒条件下：
• 3 个相邻的 1/3 倍频程可以合成 1 个 1 倍频程；
• 所有频带能量（在覆盖范围内）求和可得到总能量。
IEC 61260-1 也提到窄带分数倍频程输出可以组合近似更宽带的带级。 [1]
合成规则永远是能量域求和：

若 L_i 为各带级（dB），对应线性能量 E_i：

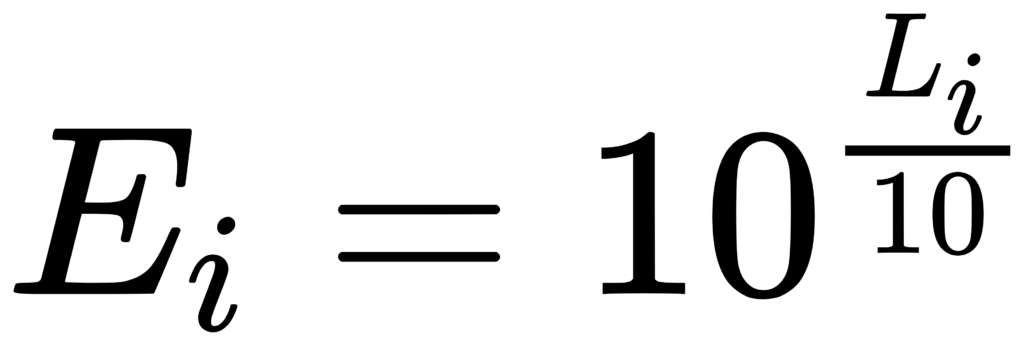
合成带级：

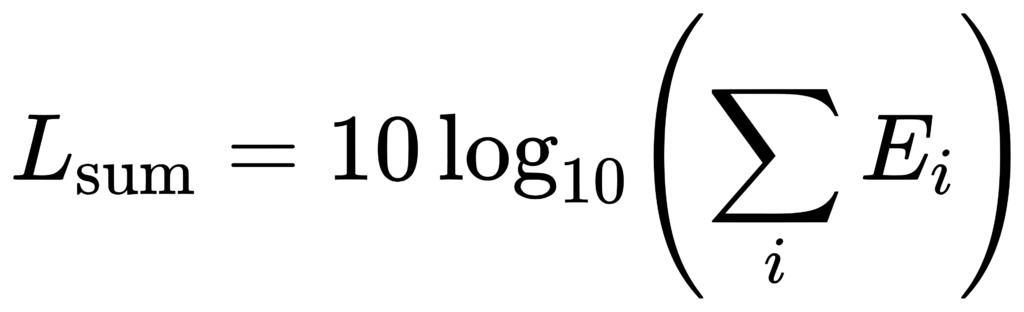
“有效带宽（effective bandwidth）”与为何标准要规定它

现实滤波器不是理想砖墙，通带起伏与边缘滚降会影响“随机噪声通过后得到的能量”。
因此标准往往引入有效带宽概念：等效成一个理想滤波器，其通过噪声功率与真实滤波器相同。IEC 61260-1 还定义了归一化有效带宽，且在定义中出现对 1/f（按对数频率度量）的权重形式。 [1]
工程意义：这保证不同实现的滤波器，在测量宽带噪声（尤其是粉红噪声类）时能得到可比的带级。

把“有效带宽”写成一行公式

以单位增益的带通滤波器 H(f) 为例，若输入是白噪声（PSD 为常数 S0），输出均方为：

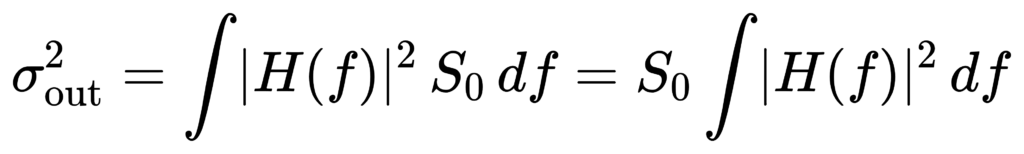
因此可以把滤波器等效成一个‘理想矩形带通’，其带宽定义为：

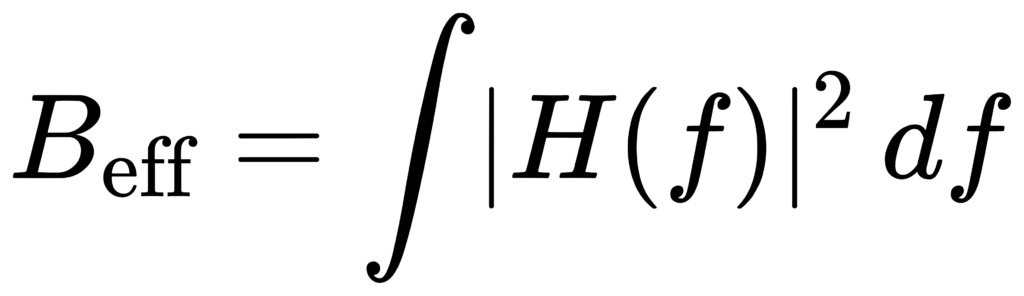
这就是最常见的有效带宽（effective bandwidth / noise bandwidth）直觉：它衡量的是‘噪声能量能通过多少’而不是‘-3 dB 点在哪里’。

如果输入不是白噪声，而更接近粉红噪声（PSD ~ 1/f），那么不同频率的噪声贡献不再等权。标准在定义归一化有效带宽时引入相应权重，目的仍然是同一个：让不同实现对‘典型工程噪声’给出可比带级。 [1]

工程上最常见的坑：
• 你用 FFT 装桶得到的带级，相当于默认了‘砖墙滤波器’（|H|^2=1/0），其 B_eff 就是 (f2-f1)。
• 你用真实 IEC/ANSI 滤波器组得到的带级，相当于用一个有滚降的 |H|^2，因此 B_eff 往往略大于 (f2-f1)，且不同 class 会不同。
所以当你要把两者对齐时，最靠谱的方法是：要么用 FFT synthesis 去逼近真实 |H|^2，要么在 FFT 装桶里引入与标准一致的过渡带权重。

为什么标准与工程界偏爱 1/3 倍频程？

1/3 倍频程的“信息密度”刚好：比 1 倍频程细、比更细分数稳

把一个 octave 只用 1 个数描述（1 倍频程）往往过粗，会掩盖谱形；但把一个 octave 切得过细（如 1/12、1/24）又会：
• 增加测量/估计方差（随机噪声下每带能量更不稳定）；
• 增加实现复杂度与计算/报告成本；
• 在多数法规与评价体系中“信息过剩”。
1/3 倍频程是经典折中：工程上足够细，统计上足够稳，生态上最普及。

心理声学因素：临界带在中频段接近 1/3 倍频程

不少心理声学资料指出，可听频段可划分为约 24 个临界带（critical bands），且在中频段临界带宽与 1/3 倍频程带宽相近。 [7][8]
这使得 1/3 倍频程在很多“与听感相关”的工程问题中成为自然的中间尺度：
• 环境噪声的频带贡献解释
• 声品质（loudness 等）计算的输入谱（部分标准/方法使用 1/3 倍频程作为输入格式）
注意：1/3 倍频程并不等同 Bark/ERB 等感知尺度，但它标准化程度更高、跨行业可比性更强。

标准与应用直接驱动：很多流程把 1/3 写死为输入/输出

当某些关键标准把 1/3 倍频程写进流程，产业链就会围绕它形成惯性。典型例子：
• 建筑隔声的评级：ISO 717-1:2020 提到实验室测量单值量计算使用 1/3 倍频程。 [5]
• 房间声学参数：混响时间等参数常按倍频程/1/3 倍频程报告（如 ISO 3382 系列）。 [6]
一旦“报告格式”变成标准要求，仪器与软件就会优先支持这种格式，从而进一步巩固其地位。

base-10 的额外工程红利：R10 表格化 + 10/decade + 易读性

• 10 bands per decade：频率每乘以 10，正好跨 10 个 1/3 带（表格与坐标轴刻度非常规整）。
• R10 优选数：1.00、1.25、1.60、2.00、2.50、3.15、4.00、5.00、6.30、8.00（乘以 10^n）几乎人人熟悉，工程沟通成本低。
• 对比 base-2：虽然更符合“octave=2”的直觉，但标称频率的十进制表达会更别扭，且跨标准/报告更容易引入歧义。

倍频程分析的实现方法，主要有FFT装桶和滤波器组法两种，继续阅读-> 倍频程分析指南：FFT装桶 vs 滤波器组法

OpenTest已集成两种倍频程分析方法，访问OpenTest 网站 www.opentest.com 下载免费版软件，更多功能与应用案例等待您的解锁。

参考文献

[1] IEC 61260-1:2014 PDF sample (iTeh): https://cdn.standards.iteh.ai/samples/13383/3c4ae3e762b540cc8111744cb8f0ae8e/IEC-61260-1-2014.pdf

[2] ISO 266:1997, Acoustics – Preferred frequencies (ISO): https://www.iso.org/obp/ui/

[3] ANSI S1.11-2004 preview PDF (ASA/ANSI): https://webstore.ansi.org/preview-pages/ASA/preview_ANSI%2BS1.11-2004.pdf

[4] ANSI/ASA S1.11-2014/Part 1 / IEC 61260-1:2014 preview: https://webstore.ansi.org/preview-pages/ASA/preview_ANSI%2BASA%2BS1.11-2014%2BPart%2B1%2BIEC%2B61260-1-2014%2B%28R2019%29.pdf

[5] ISO 717-1:2020 abstract (mentions one-third-octave usage): https://www.iso.org/standard/77435.html

[6] ISO 3382-2:2008 abstract (room acoustics parameters): https://www.iso.org/standard/36201.html

[7] Ansys Help: Bark scale and critical bands (mentions midrange close to third octave): https://ansyshelp.ansys.com/public/Views/Secured/corp/v252/en/Sound_SAS_UG/Sound/UG_SAS/bark_scale_and_critical_bands_179506.html

[8] Simon Fraser University Sonic Studio Handbook: Critical Band and Critical Bandwidth: https://www.sfu.ca/sonic-studio-webdav/cmns/Handbook5/handbook/Critical_Band.html

[9] MathWorks: ENBW definition example: https://www.mathworks.com/help/signal/ref/enbw.html