倍频程分析指南：FFT频带积分 vs 滤波器组法

2025-12-22

基于倍频程滤波器组的分析（True Octave / CPB Filter Bank）

并联滤波器 + 带内能量检测 + 时间平均

滤波器组法（常被称为 true octave analysis）是最“标准仪器化”的实现：
1) 为每个中心频率设计带通滤波器 H_b(z)（或 H_b(s)）
2) 所有滤波器并联，对输入 x(t) 同时滤波得到 y_b(t)
3) 对每个 y_b(t) 计算带内均方/功率并做时间平均，得到带级 L_b
滤波器的幅频响应需要满足 IEC/ANSI 的容差掩模（mask），以保证不同仪器可比。 [1][3]

IIR vs FIR：为什么工程上常用 IIR？

IIR 的优势：
• 对给定滚降与带外抑制，所需阶数通常远低于 FIR，计算量更低
• 适合实时仪器与嵌入式实现
• 可用级联二阶节（biquad）保证数值稳定
FIR 的优势：
• 可实现线性相位（对需要保留波形形状的应用有价值）
• 设计与验证更直接
但对“只要带级”的场景，相位通常不是主要指标，因此 IIR 是常见选择。

多速率（multirate）是 CPB 滤波器组的秘密武器

CPB 的低频带宽很窄，如果按原采样率直接实现，会浪费算力。常见做法是：
• 将频带按 octave 分组
• 对低频组先做低通 + 抽取（例如每降一个 octave 抽取 2 倍）
• 在降低采样率后的信号上实现低频 1/3 带通
这样可以显著降低滤波器阶数需求与运算量，同时保持标准定义的频带结构。

时间平均/时间加权：带级不是“瞬时值”，而是统计量

倍频程带级通常需要时间平均。常见三类：
• 块平均（block RMS）：每 T 秒输出一次
• 指数平均（exponential averaging）：等效一阶低通平滑能量
• Leq（等效连续级）：在能量域对整个测量时长积分
在声级计语境中，IEC 61672-1 描述了 Fast/Slow 等时间加权概念（Fast 典型时间常数约 125 ms，Slow 约 1 s）。 [5][6]
工程含义：同一个频带，如果你用不同时间常数，读数会不同；报告必须注明时间加权。

如何验证滤波器组“像标准那样工作”？

正弦扫频：检查每个频带在其通带内的响应与邻带隔离；也能观察瞬态/群延迟导致的滞后
粉红噪声/白噪声：检查带级是否与理论谱（1/f 或常数 PSD）一致；同时可估计带级方差与稳定时间
脉冲/阶跃：检查滤波器的时域振铃与时间响应（对瞬态应用尤其重要）
对照法：用已知“符合 IEC/ANSI 的参考实现/仪器”对同一信号比对带级

从“定义频带”到“做出合规数字滤波器”的完整流程

如果你需要自己实现一个“接近标准仪器”的 1/3 倍频程滤波器组，可以按下面的工程流程走（不依赖某个特定软件）：

确定频带体系：选 base-10/base-2、选 1/b（通常 b=3），用 exact 公式生成全部中心频率 fm 与边界 f1/f2
确定性能目标：你要对标哪个标准版本/哪个 class？这会影响你允许的通带起伏、边缘滚降斜率、以及邻带隔离
选择滤波器结构：实时/嵌入式常用 IIR（biquad 级联）；若对相位敏感或要离线零相位，可考虑 FIR 或前后向滤波
设计单个频带：以 f1/f2 为关键频率，设计带通；注意数字域频率映射可能需要预失真（例如双线性变换的 pre-warp）来让数字滤波器的边界落在你期望的位置
做全带覆盖与多速率：把频带按 octave 分组，低频组先低通+抽取；抽取前必须有足够的抗混叠滤波
验证：逐带检查幅频响应是否落在标准 mask 允许范围；用噪声验证有效带宽与带级偏差；用扫频/脉冲验证时间响应
定标与单位：确认输入单位（Pa、m/s^2 等）与参考量（20 µPa 等）；确认 RMS/Leq 的时间平均与报告口径

时间响应：群延迟、振铃、时间平均三者如何共同决定“读数”

倍频程带级看起来是频域量，但在真实仪器里它是‘滤波 + 能量检测 + 平滑’的时域系统，所以会出现三个时间尺度：
• 滤波器本身的群延迟：决定一个事件在该频带上“晚多久”出现
• 滤波器的振铃/衰减时间：决定一个短脉冲会在该频带上拖尾多久
• 你选的时间平均（Fast/Slow/Leq 或滑动 RMS）：决定你输出的时间分辨率与抖动
当你用倍频程去看瞬态（冲击、开关噪声、扫频起停），不同实现即便都满足同一幅频 mask，也可能给出不同的峰值与时间轨迹——这正是 ANSI 提醒的原因。 [3]

一个非常实用的经验：
• 想看‘稳态频带贡献’：加长平均时间，让结果更稳定（更像法规测量）
• 想看‘瞬态在哪个频带爆发’：缩短平均时间，但必须接受更大波动，并固定滤波器实现（尤其是阶数/相位特性）

实时实现常见坑

• 抽取链路忘记抗混叠：低频带级会被混叠污染，且很难肉眼看出来
• biquad 系数数值问题：高 Q（细分数）在低频时系数可能很极端，需要用双精度或 SOS 结构避免不稳定
• 直接对 dB 做平均：必须先在能量域平均，再转 dB
• 频带重叠导致‘总能量不守恒’：真实标准滤波器并不要求功率互补，别用“各带加和=总级”去强行判错；应以标准口径与参考实现对齐为准

使用OpenTest进行基于倍频程滤波器组的分析

OpenTest支持基于倍频程滤波器组的分析：
1) 连接设备，如SonoDAQ Pro
2) 勾选通道并调整参数设置，如外接麦克风，需开启IEPE，并切换到声信号测量
3) 在测量模式的倍频程分析板块中，选择IEC 61260-1算法，支持实时分析、线性平均、指数平均、最大保持
4) 在参数配置完成后，点击测试按钮即可开始测试
5) 支持一次录制同时分析1/1倍频程、1/3倍频程、1/6倍频程、1/12倍频程、1/24倍频程

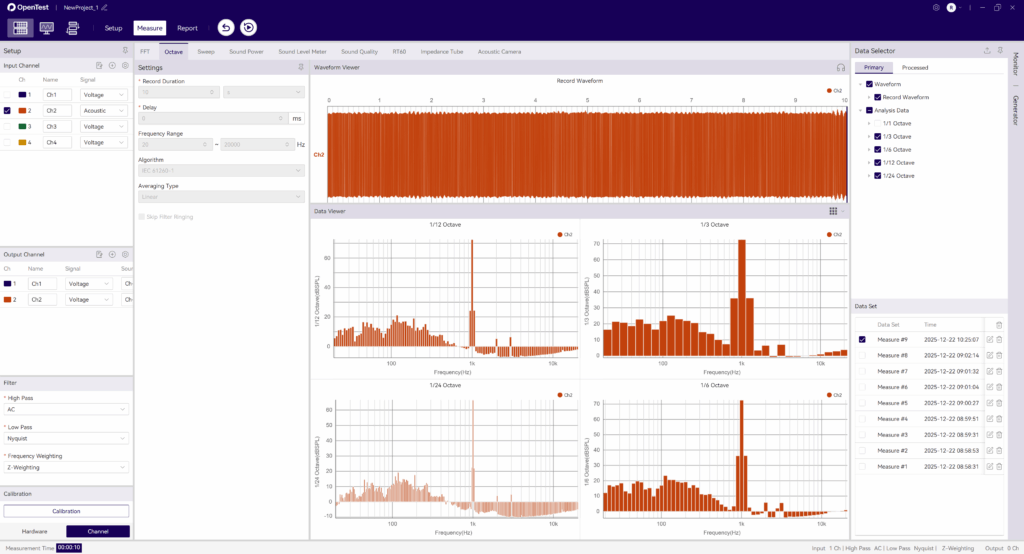
图 1：使用OpenTest进行基于倍频程滤波器组的分析

使用OpenTest的IEC 61260-1倍频程分析功能观察数据->

FFT 频带积分与 FFT Synthesis（频域合成）

FFT 频带积分的本质：把线谱变成 CPB 频带积分

FFT 法通常包含两步：
1) 先做谱估计：单帧 FFT、Welch 平均、或 STFT（重叠短时 FFT）得到 |X[k]|^2 或 PSD[k]；
2) 对每个倍频程频带，求和/积分得到带功率 P_band。
它在软件和离线处理中很常见：一次 FFT 可以得到全频段细粒度谱，随后“频带积分”为任意频带体系（1/1、1/3、1/12…）。

关键难点一：FFT 的尺度（scaling）和窗函数校正

做 FFT 之后，你拿到的 |X[k]| 是“与实现定义相关”的量：是否做了 1/N 归一化？是幅度谱还是功率谱？是否单边谱？
更关键的是窗函数：窗会改变能量分布与噪声底。要在 PSD 口径下正确积分，需要考虑窗的等效噪声带宽（ENBW）。
ENBW 的一个常见定义形式：ENBW = fs * sum(w^2) / (sum(w))^2。 [7]
工程落地：如果你在噪声测量中忽略 ENBW，你的 PSD 与带级会出现系统性偏差，尤其是在宽带噪声下。

一个常用且不容易错的 PSD 归一化写法（用于频带积分积分）

以单帧 periodogram 为例（Welch 只是对多帧做平均），一种常见定义是：

X[k] = FFT( w[n]·x[n] )
U = (1/N) · Σ w[n]^2
PSD_two_sided[k] = |X[k]|^2 / (fs · N · U)

然后再转为单边 PSD：除 DC/Nyquist 外乘以 2。这样做的好处是：
• PSD 的单位是‘输入单位^2/Hz’（例如 Pa^2/Hz），
• 对白噪声，其 PSD 平均值与理论常数一致（只差统计波动），
• 对 PSD 做 Σ PSD·Δf 可以回到均方（RMS^2），便于与时域结果交叉验证。

两个最实用的“自检”方法：一眼看出你的 scaling 有没有错

自检 A（白噪声）：生成一段已知方差 σ^2 的白噪声，理论上其总均方应接近 σ^2。你把 PSD 在 0..fs/2 积分（单边谱要包含乘 2 规则）应回到同一个 σ^2。
自检 B（纯音）：生成一个幅值 A 的正弦（注意 RMS= A/√2），其能量应几乎集中在一个或少数几个 bins（取决于是否整周期与窗函数）。把频域能量积分回去，应该接近 (A^2/2)。
只要这两项对上了，你的 FFT scaling 大概率是正确的；之后再谈 ENBW、partial-bin、倍频程频带积分才有意义。

关键难点二：bin 与频带边界不对齐 -> 需要“部分 bin”加权

1/3 倍频程边界通常不会恰好落在 FFT 的 bin 频率上。若你简单地“包含或排除某个 bin”，会造成阶梯状误差。
更严谨的做法是：对边界处的 bin 按其频率覆盖比例做部分面积加权（相当于把 PSD 在 bin 内视为常数并做截断积分）。
这在低频尤其重要，因为低频带宽窄，落在边界的那几个 bin 占比更大。

“部分 bin”加权的最小实现（伪代码级别，可直接落地）

假设你有单边 PSD 数组 PSD[k]，对应每个 bin 的中心频率 f_k = k·fs/N，bin 宽度 Δf=fs/N。对某个倍频程频带 [f1,f2]：
1) 找到完全落入频带内部的 bins：这些 bins 的权重 α_k=1；
2) 对落在边界附近的最多两个 bins，计算重叠比例 α_k∈(0,1)；
3) 带内均方 = Σ α_k · PSD[k] · Δf。
注意：如果你用的是双边谱，f_k 的定义与边界处理会不同；但‘重叠比例’这一思想是通用的。

零填充（zero-padding）能解决边界不对齐吗？

零填充能让频谱曲线看起来更平滑（相当于在频域做插值），但它并不会真正提高频率分辨率：真实分辨率仍由原始窗长决定。
因此，对倍频程频带积分而言：
• 零填充可以让边界落在更细的频点上，从而减小‘截断误差’的视觉跳变；
• 但如果 N 太小导致低频每带只有 1-2 个 bins，再怎么零填充也不会变成“可靠的低频带级”。
根本解决方案仍然是：足够长的窗（更细 Δf）或采用多速率/滤波器组方法。

关键难点三：时间-频率折中（窗长决定低频精度与延迟）

FFT 分辨率 Δf = fs/N。低频 1/3 带宽很窄：例如 20 Hz 这一带的带宽只有几 Hz。若希望每带至少 10 个 bins，则 Δf 需小于带宽/10，这会要求 N 很大，从而带来：
• 更大的延迟（至少一个窗长）；
• 对非平稳信号的时间平滑（瞬态被“拉长”）。
因此：FFT 频带积分在“稳态噪声的统计带级”上很优秀，但在“快速变化/瞬态的带级轨迹”上可能不如滤波器组直观。

低频难题的根源：1/3 倍频程是常数-Q，但 STFT 是常数-Δf

这是很多人第一次做低频 1/3 倍频程时会“踩坑”的根本原因：
• 1/3 倍频程的带宽 Δf_band 与中心频率成正比（常数-Q）；
• STFT/FFT 的 bin 宽度 Δf_bin 是常数（常数-Δf）。
因此在低频，你需要非常小的 Δf_bin 才能把窄频带切得足够细；在高频反而绰绰有余。

解决路线对比：长窗 STFT vs 多速率 STFT vs CQT/小波

常见三条路线：
• 长窗 STFT：实现最简单，但延迟大、瞬态被拉长。
• 多速率 STFT：低频先抽取再做 FFT，用较小采样率实现更细的低频 Δf；与 6.3 的多速率滤波器组思路一致。
• 常数-Q 变换（CQT）/小波：天生就是对数频率分辨，更接近倍频程带；但若要严格对标 IEC/ANSI 的滤波器 mask，需要额外校准与验证。 [4]
工程上：合规测量优先‘标准滤波器组’；科研/特征提取则可以考虑 CQT/小波等更灵活的方法。

FFT Synthesis：用频域权重构造“每带滤波”

FFT synthesis（频域合成）可以把 FFT 法推向“滤波器组”的方向：
• 为每个频带构造频域权重 W_b[k]（可近似标准滤波器的幅频掩模，或用更平滑的过渡带）；
• 令 Y_b[k] = X[k] * W_b[k]；
• IFFT 得到 y_b[n]，再计算带内 RMS/平均。
特点：
• 容易实现零相位（非因果）滤波；
• 可用 overlap-add 做流式输出，但依然有块延迟；
• 若要严格符合 IEC/ANSI 的掩模，需要精心设计 W_b 与验证。

FFT Synthesis 做成“流式倍频程仪器”的关键：OLA、双窗与幅度归一化

如果你希望 FFT synthesis 不只是离线块处理，而是像仪器一样连续输出，每一步都要把“块”拼回“流”：
• 分帧：以 hop 为步长取帧并加分析窗 w_a[n]；
• 频域加权：Y_b[k]=X[k]·W_b[k]；
• IFFT 得到 y_b[n] 后，再乘合成窗 w_s[n] 并 overlap-add；
• 选择 w_a 与 w_s 使得重叠相加满足近似恒等（COLA 条件），否则带内 RMS 会随帧对齐产生周期性起伏。
这也是为什么很多实现会固定窗型与重叠率（例如 Hann + 50% 重叠）并在最后做幅度归一化。

如果目标是“对标标准滤波器”，W_b[k] 应该如何选？

W_b[k] 的选择取决于你追求的‘像什么’：
• 追求砖墙积分一致性：W_b[k] 直接取 0/1（硬边界），最接近频带积分。
• 追求与 IEC/ANSI 滤波器一致：让 |W_b(f)| 逼近标准规定的幅频掩模，并关注有效带宽（相当于匹配 ∫|W_b|^2）。
• 追求可重构/能量守恒：让各带权重满足近似功率互补 Σ|W_b(f)|^2≈1。
三者通常不能同时完美满足，所以实现前先明确目标会省掉很多返工。

能量守恒的频域滤波器组：为什么要关心 Σ|W_b|^2？

如果你的目标是“每带能量可加、总能量守恒”，一个常见的设计原则是让频域权重满足（近似）功率互补：
Σ_b |W_b(f)|^2 ≈ 1（在分析频段内）。
这样对于宽带信号，按 Parseval 定理，各带能量之和接近总能量（忽略边缘与数值误差）。
注意：IEC/ANSI 的真实滤波器掩模不一定满足严格互补，因此你需要明确你的目的：合规测量 vs 信号分解/重建。

Welch/平均策略：如何让 FFT 带级更稳？

Welch 平均：分段、加窗、重叠、对功率谱平均，是噪声 PSD 估计的常用办法。
时间平均要在功率域做：平均 |X|^2 或 PSD，再转 dB。
对非平稳信号：考虑用 STFT 输出时间-频带矩阵（类似声级计的时间序列）。
报告时说明：窗类型、重叠率、平均次数、是否做了 ENBW/幅度校正。

使用OpenTest进行FFT频带积分分析

OpenTest支持基于FFT装桶的倍频程分析：
1) 连接设备，如SonoDAQ Pro
2) 勾选通道并调整参数设置，如外接麦克风，需开启IEPE，并切换到声信号测量
3) 在测量模式的倍频程分析板块中，选择基于FFT分析的算法
4) 支持一次录制同时分析1/1倍频程、1/3倍频程、1/6倍频程、1/12倍频程、1/24倍频程

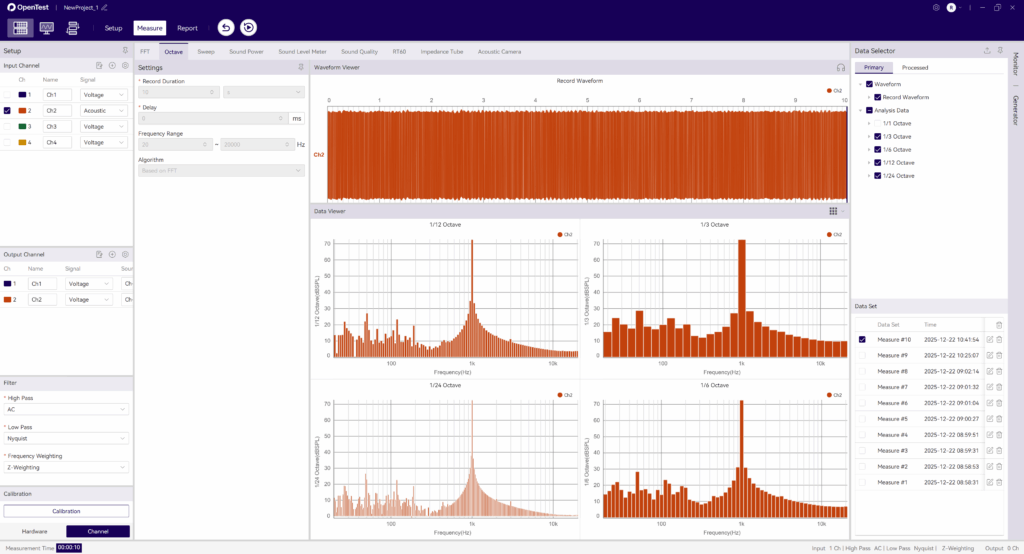
图 2：使用OpenTest进行基于FFT装桶的倍频程分析

使用OpenTest的FFT装桶倍频程分析功能观察数据->

倍频程滤波器法 vs FFT/FFT Synthesis：差异、等价条件与工程取舍

核心差异

维度	滤波器组法（True Octave/CPB）	FFT 装桶 / FFT Synthesis
标准符合性	更容易严格对标 IEC/ANSI 的幅频掩模；硬件仪器主流路线。 [1][3]	若仅装桶，更像“频带积分”；要严格匹配掩模需额外设计权重或用标准化数字滤波器。
实时性/延迟	可因果实时；延迟由滤波器阶数与时间平均决定。	块处理至少一个窗长延迟；低频为了分辨率往往需要更长窗。
瞬态响应	输出随时间连续变化，但受滤波器群延迟/振铃影响；不同合规实现可能不同。 [3]	由 STFT 窗决定时间扩展；瞬态被窗平滑，且对窗类型/长度敏感。
泄漏与校正	带外抑制主要靠滤波器设计，泄漏可控。	强依赖窗函数与 ENBW/幅度校正；边界 bin 不对齐需部分加权。 [7]
可解释性	对应“通过某个带通滤波器后的 RMS”，与声级计/分析仪一致，解释直观。	对应“谱估计 + 装桶”，更接近统计谱分析；解释需结合窗长与平均方式。
计算量	多滤波器并行；多速率可降成本。	一次 FFT 可复用所有频带；离线/批量处理效率高。
相位与可重建性	IIR 一般非线性相位（但对带级无碍）。	频域权重可做零相位（非因果）；若做带信号重建，需关注权重互补与边缘过渡。

什么时候两者会给出“几乎一样”的结果？

在以下条件同时满足时，滤波器法与 FFT 装桶法的平均带级通常非常接近：

信号近似平稳（stationary），且观测时间足够长；
FFT 分辨率足够细：每个频带含足够多 bins（尤其最低频带）；
窗函数的幅度/能量尺度、单边谱、ENBW 等做了正确校正；
频带边界处做了部分 bin 加权，而不是粗暴截断；
只比较统计意义上的平均带级，不比较瞬态随时间变化的轨迹。

为什么在瞬态/短时事件中差异会变大？

差异放大的根本原因是“时间尺度不一致”：
• 滤波器组法：每个频带有自己的群延迟与振铃，但可以连续输出；
• FFT/STFT：用固定窗长做局部谱估计，窗长既决定频率分辨率，也决定时间平滑与延迟。
当事件持续时间与窗长/滤波器时域响应同一个量级时，结果会明显依赖具体实现。因此，做瞬态诊断时应尽量固定算法细节，并用基准信号做一致性验证。

误差预算（error budget）：两种实现差异通常从哪里来？怎么快速定位？

当你发现“滤波器组 vs FFT 装桶”对不齐时，不要盲目调参数。建议按影响从大到小做排查（越靠前越常见）：

dB 平均/合成方式是否错误：是否在能量域平均与求和？（这是最常见的‘一票否决’问题）
FFT scaling 是否一致：1/N 归一化、单边/双边、Δf、窗函数 U（sum(w^2)）是否匹配？
窗函数校正是否匹配：噪声测量是否用 ENBW，纯音幅度是否考虑 coherent gain？
频带边界是否按 exact 计算：是否误用 nominal 频率去算 f1/f2？
边界 bin 是否做 partial-bin 加权：低频带宽窄时差异会被放大。
滤波器组是否多速率：抽取链路是否抗混叠充分？不同抽取方案会影响带外能量泄漏。
时间平均是否一致：块长、重叠、指数时间常数是否一致？
真正的‘标准差异’：若你在对标某个 class 的 mask，FFT 装桶（砖墙）与真实滤波器（滚降）本来就可能有系统差。

一个很有效的定位方法：先用白噪声把总均方、每带均方对齐（排除 scaling/ENBW/partial-bin 问题），再用扫频/纯音检查频带中心与邻带隔离（排除频带定义与滤波器实现问题）。

工程落地清单：如何把 1/3 倍频程做对、做稳、做可复现

选方法：合规测量优先滤波器组；离线统计可优先 FFT 装桶

若目标是法规/型式试验/仪器一致性：优先使用符合 IEC/ANSI 的倍频程滤波器组实现，并注明 class 与标准版本。 [1][3]
若目标是离线分析、大批量数据、希望灵活切换频带：FFT 装桶更高效，但必须把尺度校正与边界加权做严谨。
若目标是“得到每带时域信号”（例如后续做调制分析、包络等）：可考虑 FFT synthesis 或 FIR/IIR 滤波器组。

FFT 装桶的参数选取：从最低频带推 N（示例）

假设 fs=48 kHz，最低关注 20 Hz 的 1/3 倍频程。其带宽约为：Δf ≈ f2-f1 ≈ 4.6 Hz（见附录表）。
若你希望该频带至少有 M=10 个 bins，则需要 Δf_bin = fs/N <= 4.6/10 ≈ 0.46 Hz，即 N >= 48000/0.46 ≈ 104000 点。工程上通常选最近的 2^n：N=131072。
这就是为什么“用 FFT 做低频 1/3 倍频程”常会带来很大窗长与延迟。

典型错误清单

把幅度谱 |X| 相加当成能量：必须用 |X|^2（或 PSD）在功率域求和。
直接平均 dB：所有平均/合成都应先回到线性功率/均方域，再转 dB。
忽略窗函数校正与 ENBW：宽带噪声下会出现系统偏差。 [7]
用 nominal 频率算边界：边界应基于 exact 计算，再用于标注为 nominal。
不说明时间平均方式：Fast/Slow/Leq 对结果影响很大。 [5][6]

报告与可复现信息清单：把这些写进报告，别人就能复算你的带级

倍频程结果最大的风险不是“算错一次”，而是“别人复现不出来”。下面给一份强烈推荐写进报告/测试记录的清单（尤其是你需要对标标准或跨团队交付时）：

频带定义：base-10 还是 base-2？1/b 的 b 是多少？使用 exact 还是 nominal 作为计算依据？参考频率 fr 是多少？
实现方法：标准滤波器组（IIR/FIR、多速率与否）还是 FFT 装桶/FFT synthesis？软件版本/库版本。
采样与预处理：采样率 fs、是否做了去直流/去趋势、是否做了防混叠滤波、是否做了重采样。
时间平均：Leq/块 RMS/指数平均？时间常数/块长/重叠率/平均帧数？是否采用 Fast/Slow 等时间加权？
FFT 细节（若使用）：窗类型、N、hop、是否零填充、PSD 归一化公式、单边谱处理、ENBW/CG 校正、partial-bin 加权方式。
校准与单位：输入量纲（Pa、m/s、m/s^2）、参考量（20 µPa 等）、传感器校准因子与日期。
输出口径：每带是 RMS、峰值、还是带功率？dB 是 10log 还是 20log（对功率/幅度不要混用）？是否做了频带合成？

如果你只想记一句话：把“频带定义 + 时间平均 + FFT scaling/窗校正（若有）”写清楚，90% 的争议都会消失。

快速公式与数值例（可直接拿去写代码/报告）

10.1 base-10 1/3 倍频程的常用常数

G = 10^(3/10) ≈ 1.995262
r = 10^(1/10) ≈ 1.258925 (相邻中心频率比值)
k = 10^(1/20) ≈ 1.122018 (边界相对中心倍数)
f1 = fm / k
f2 = fm * k

10.2 1 kHz 频带边界示例

fm = 1000 Hz
f1 = 1000 / 1.122018 ≈ 891.25 Hz
f2 = 1000 * 1.122018 ≈ 1122.02 Hz
Δf ≈ 230.77 Hz
Q ≈ 4.33

OpenTest已集成两种倍频程分析方法，访问OpenTest 网站 www.opentest.com 下载免费版软件，更多功能与应用案例等待您的解锁。

参考文献

[1] IEC 61260-1:2014 PDF sample (iTeh): https://cdn.standards.iteh.ai/samples/13383/3c4ae3e762b540cc8111744cb8f0ae8e/IEC-61260-1-2014.pdf

[3] ANSI S1.11-2004 preview PDF (ASA/ANSI): https://webstore.ansi.org/preview-pages/ASA/preview_ANSI%2BS1.11-2004.pdf

[4] HEAD acoustics Application Note: FFT – 1/n-Octave Analysis – Wavelet (filter bank description): https://cdn.head-acoustics.com/fileadmin/data/global/Application-Notes/SVP/FFT-nthOctave-Wavelet_e.pdf

[5] IEC 61672-1:2013 (IEC page): https://webstore.iec.ch/en/publication/5708

[6] NTi Audio Know-how: Fast/Slow time weighting (IEC 61672-1 context): https://www.nti-audio.com/en/support/know-how/fast-slow-impulse-time-weighting-what-do-they-mean

[7] MathWorks: ENBW definition example: https://www.mathworks.com/help/signal/ref/enbw.html

2025-12-22