2026-01-05
FFT分析指南:从时间波形到频率谱,一眼看透信号
在声学与振动测试里,FFT 分析(Fast Fourier Transform,快速傅里叶变换)几乎是每位工程师都会打开的工具,做扬声器频响、耳机失真、NVH 诊断、结构共振排查、产线异常噪声定位……
很多工程问题其实都在问同一件事:能量主要集中在哪些频率?是一个主频还是一堆谐波?噪声底高不高?有没有共振峰?FFT 是回答这些问题的最通用入口。
本文帮助你从工程视角理清三件事:
- 什么是FFT分析
- FFT分析的工作原理
- 如何正确且高效地使用FFT
什么是 FFT?
在时间域里,一个信号就是一条随时间变化的波形——所有成分都“挤在一起”,看得见,却难以分辨里面到底有哪些频率。
FFT(Fast Fourier Transform,快速傅里叶变换)的作用,就是把时间信号分解成一系列不同频率的正弦波,在频率域里用“频率 + 幅值 + 相位”来描述原始信号。简单理解:
- 时间域:看到的是“这段时间里信号怎么跳来跳去”
- 频率域:看到的是“里面都有哪些频率成分、哪个最强、相互之间什么关系”
傅里叶最初(19 世纪初)提出的核心思想是:复杂的周期函数可以分解成一堆正弦/余弦的叠加。后来发展成连续时间的傅里叶变换,把信号映射到连续的频率轴。
计算机时代改变了一切:工程师拿到的是采样数据,而且只拿到有限长度 N 的一段。于是出现了 DFT(离散傅里叶变换):把 N 个采样点变成 N 个离散频点的复数值。
而FFT(快速傅里叶变换)并不是“另一种变换”。它是一类算法家族,用更快的方式计算完全相同的 DFT 结果,也就是 “用巧妙的分治和对称性复用”,把同一个 DFT 的计算从 O(N²) 降到 O(N log N);你得到的 X[k] 与直接算 DFT 完全相同,只是快得多。
FFT擅长什么?不擅长什么?
FFT 很擅长:
- 找确定性的窄带成分:主频、谐波、开关频率、啸叫点、机械转速相关峰
- 看宽带分布:噪声底、谱倾斜(1/f)、带内功率(band power)、SNR
- 做系统特性分析:传递函数、共振/反共振、相干函数、延迟估计
- 做时间-频率分析的基石:STFT/声谱图
FFT 不擅长(或不能单靠它解决)的典型场景:
- 强非平稳信号的“瞬时频率”问题:必须用 STFT/小波/时频方法,而不是指望单次 FFT
- 区分两个极近的正弦:如果它们间隔小于你的分辨率(由 N 决定),再聪明也分不开
- 把短记录“变成长记录”:零填充只能让曲线更平滑(插值),不会凭空增加信息
想把 FFT 用好,先搞清这些概念
采样率:你能看到多高的频率
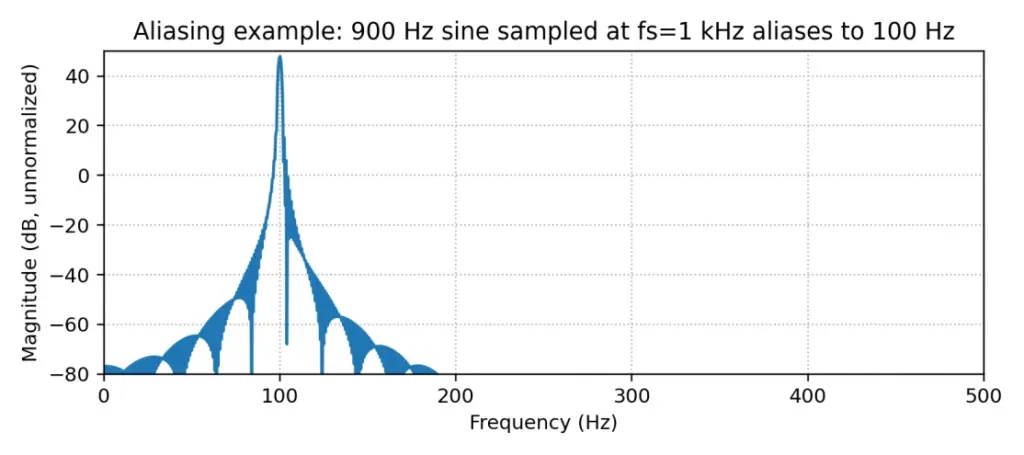
在做任何 FFT 之前,你首先做了采样:从连续时间信号 x(t) 变成离散序列 x[n] = x(n/fs)。采样率 fs 决定了你能观察到的最高无混叠频率:Nyquist 频率 = fs/2。
如果模拟信号里存在高于 fs/2 的成分,它不会“消失”,而是折叠到低频,形成混叠(aliasing)。混叠一旦发生,后面再怎么 FFT 都救不回来。工程上必须在 ADC 前(或重采样前)用抗混叠滤波器把高频压下去。
DFT计算
给定 N 个采样点 x[0]..x[N-1],DFT 定义为:
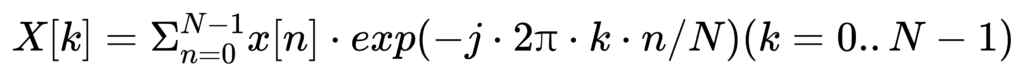
逆变换(IDFT):
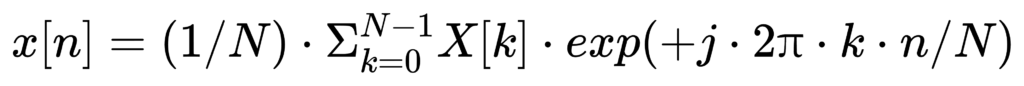
直觉理解:X[k] 可以看成 x[n] 与某个复指数 e^{j2πkn/N} 的相关程度;幅度告诉你“有多少”,相位告诉你“在时间上怎么对齐”。
画什么?幅度谱、幅值谱、功率谱、PSD
同样一段 FFT 输出 X[k],你可以画出很多“看起来像频谱”的东西。问题在于:它们不是同一个量,单位也不同。很多跨工具对比失败,本质是“你画的不是同一种谱”。
| 量的名称 | 常用符号 | 单位示例(若 x 是电压 V) | 最适合用来做什么 |
| 幅度谱(Magnitude spectrum) | |X[k]| | V·sample(取决于归一化) | 找主频/谐波/尖峰位置 |
| 幅值谱(Amplitude spectrum) | A(f) | V(做了正确 scaling 后) | 估计纯音幅值/校准幅度 |
| 功率谱(Power spectrum) | |X[k]|² | V²·sample²(仍依赖 scaling) | 能量对比、谱形比较(需统一约定) |
| 功率谱密度 PSD | Sxx(f) | V²/Hz | 噪声分析、带内功率/带级、跨 N 可比 |
关键结论:如果你要比较不同 N、不同窗、不同工具下的噪声水平,优先用 PSD(x²/Hz)。原始 |X| 或 |X|² 往往不可直接比。
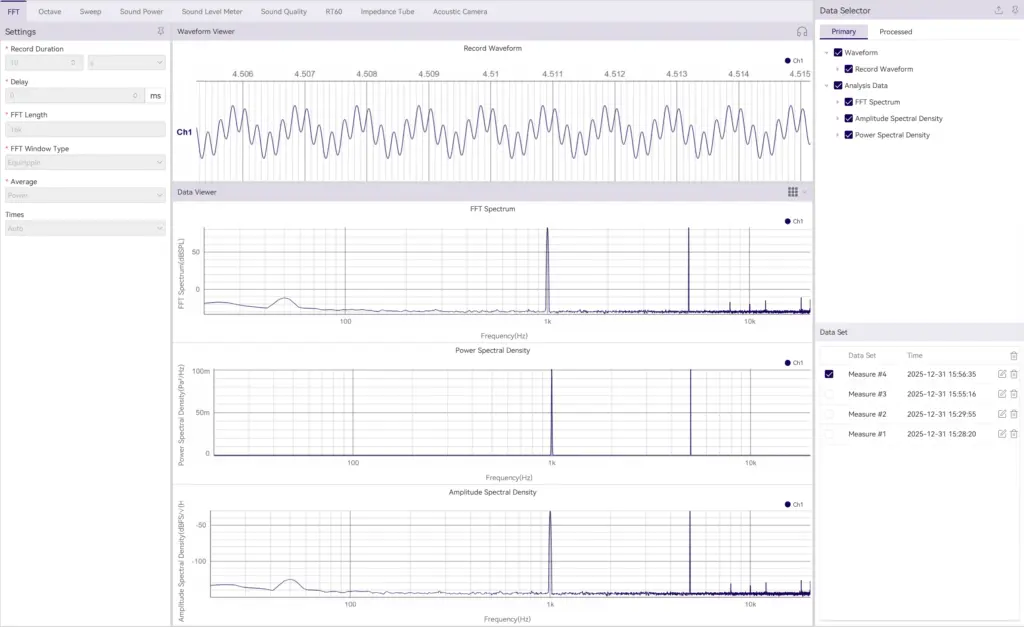
通过一个具体的例子看看:同一段信号,时域和PSD长什么样
下图中的例子包含了两个不同频率的正弦波信号。时域看起来像“抖动的波形”,频域分析后可以清楚看到两个窄峰。
窗函数与谱泄漏:让谱线更“干净”
理想情况下,FFT 假设截取的是一个完整周期并周期延拓的信号。但实际测试中采样窗口往往只截到非整数个周期,拼接时在边界产生不连续,就会导致能量“洒”到邻近频点上,这就是谱泄漏(spectral leakage)。
为减小泄漏,通常需要在做 FFT 前对时间信号乘以窗函数。窗函数会同时改变三件事:
- 主瓣宽度:主峰变宽,近邻频率更难分开
- 旁瓣高度:旁瓣越低,强峰旁边越容易看到弱峰(动态范围更好)
- 幅度/能量标定:窗会改变纯音幅度与噪声底,需要对应校正
从经验上来看常见的窗选择方向:
- Rectangular:只在你能保证相干采样(整周期)且追求最窄主瓣时使用
- Hanning:最通用、最“少出错”的选择,适合 PSD/Welch、声学/振动一般分析
- Hamming:与 Hanning 类似,通信等场景常用,旁瓣/主瓣权衡略不同
- Blackman / Blackman-Harris:旁瓣更低,适合强峰旁边找弱峰,但主瓣更宽
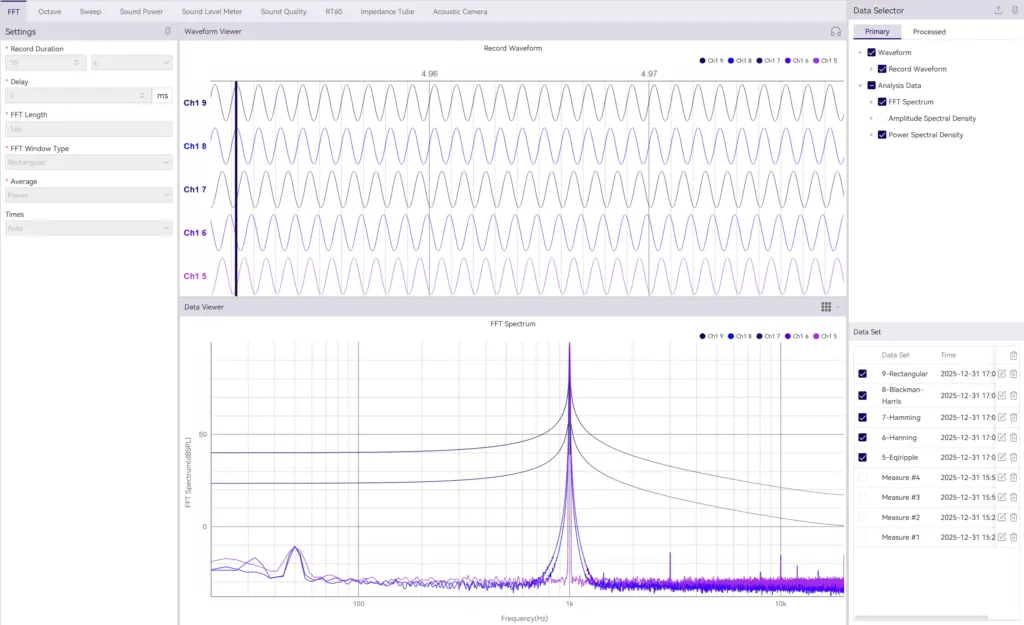
平均方式:让频谱更稳定
对噪声或非平稳信号,单次 FFT 谱往往波动很大。通过多次平均可以得到更平滑、可重复的频谱。常见方式包括:
- 线性平均:多次 FFT 结果直接算平均值
- 指数平均:给最近的数据更高权重,适合实时监控
- 能量平均:基于能量加权,保证功率相关量的一致性
合理的平均设置能在“平滑掉随机波动”和“保留真实变化”之间找到平衡。
FFT 可以用在什么测试场景里?
音频与声学
音频/声学里 FFT 常见用途:
- 找啸叫点、谐波失真、设备噪声底(PSD)
- 做频响(传递函数)、房间模态/共振分析
- 做声谱图:语音/音乐/设备噪声的时变特征
注意:声学报告里常用 dB SPL、A 计权、1/3 倍频程等。FFT 只是基础工具,输出口径(参考值、加权、带宽)一定要写清楚。
振动与旋转机械
- 找转速相关峰(1X、2X…)、齿轮啮合频率、结构共振。
- 轴承故障常需要包络分析/解调:先带通滤波再做 FFT(频域诊断链条更长)。
如果转速在变,直接 FFT 会把峰“抹开”。此时更适合做阶次分析(order tracking)或同步重采样,让频率轴变成“阶次轴”。
电力电子与电能质量
- 工频谐波(50/60 Hz 及其倍频)、THD、纹波与开关频率尖峰。
- EMI 预分析:看谱线、噪声底、带宽内能量(配合 RBW/平均)。
电力系统常见问题是“非相干采样”:记录长度不是整数个工频周期会造成泄漏,导致谐波测量偏差。工程上常用同步采样、整周期窗、或专门的谐波分析方法。
射频与通信(以基带视角)
- 看调制信号的功率谱/频谱掩模(spectral mask)。
- OFDM 等多载波信号:频域幅度统计、邻道泄漏、EVM 相关分析。
通信里更强调“单位一致、带宽一致、平均方式一致”。FFT 本身容易做,但把它变成“可比的功率谱测量”要严格定义窗、RBW、检测器与平均。
成像与 2D 滤波
图像的 2D FFT 是空间频率分析:边缘=高频,平滑=低频。
常见操作包括:频域低通/高通、去周期噪声(在频域抑制某些尖峰)、卷积加速。
注意边界:2D FFT 默认周期延拓,图像边缘不连续会引入很强的频域伪影。常用 padding、镜像边界或 2D 窗来缓解。
让 FFT 成为“顺手的工程工具”
从原理上看,FFT 涉及的数学不算轻松;但落到工程应用,目标其实很简单:
让你更快、更清楚地看懂信号里“藏着什么”。
把 FFT 从“数学概念”变成“日常顺手的工程工具”,帮助声学与振动工程师在研发、验证和生产的各个阶段,更高效地完成测试与分析工作。
OpenTest中的FFT分析现开放免费试用,立即下载使用-> 或填写下方表单 ↓ 预约演示体验。
访问OpenTest 网站 www.opentest.com 了解更多功能与应用案例。
阅读更多

OpenTest ISO 3744 声功率测试流程

OpenTest 多品牌采集卡统一接入指南

